Bonnie Evans | July 27, 2022 | Updated on: July 27th, 2022

Roulette Expected Value & Probability Explained

Expected value in roulette can be defined as the weighted average of how much you can win or lose in one full session. And, in order to calculate the expected value, players will need to know four things: the probability of winning, and the amount you’ll win if your bet gets drawn, as well as the probability of losing and the amount you’ll lose if you do.

You can insert actual amounts of money in your calculations if you’re calculating the expected value of one particular bet. Otherwise, general units can be used for calculations that cover bets of any size.

Because the American roulette wheel has 38 pockets of equal size, calculating the probability of the ball landing in either of the pockets is simple. Where the ball lands are based on chance, which means that the wheel has a uniform probability distribution.

Best Roulette Online Casinos

1

$5000 Bonus + Min Deposit: $20

No Code Required

Bonus Code

350% match bonus based on first deposit of $25+. Additional bonuses.

Play Now

Read Review

T&Cs Apply

New players only. Welcome Bonus - 500% bonus on your first deposit up to $5000 Unless otherwise stated. This bonus only applies for deposits of $25 or higher! All you need to do is just deposit the money in your casino account and you will receive this bonus instantly!

*New users only

2

$4000 bonus + Min Deposit: $10

No Code Required

Bonus Code

250% match bonus based on first deposit of $10+. Additional bonuses.

Play Now

Read Review

T&Cs Apply

New players only. Welcome Bonus - 100% bonus on your first deposit up to $4000 unless otherwise stated. This bonus only applies for deposits of $35 or higher! All you need to do is just deposit the money in your account and you will receive this bonus instantly!

*New users only

3

$5500 Bonus + Min Deposit: $25

No Code Required

Bonus Code

100% match bonus based on first deposit of $20+. Additional bonuses.

Play Now

Read Review

T&Cs Apply

New players only. Welcome Bonus - 100% bonus on your first deposit up to $5000 Unless otherwise stated. This bonus only applies for deposits of $20 or higher! All you need to do is just deposit the money in your casino account and you will receive this bonus instantly!

*New users only

1

$5000 Bonus

Min Deposit: $20

Min Deposit: $20

Min Deposit: $20

Play Now

Read Review

$5500 Bonus Min Deposit: $25 - Min Deposit: $25

2

$4000 Bonus

Min Deposit: $10

Min Deposit: $10

Min Deposit: $10

Play Now

Read review

$4000 Bonus Min Deposit: $10 - Min Deposit: $10

3

$5500 Bonus

Min Deposit: $10

Min Deposit: $10

Min Deposit: $25

Play Now

Read Review

$5500 Bonus Min Deposit: $25 - Min Deposit: $25

4

Bonus up to:
$3000
100 Free Spins
No deposit required to claim the 100 free spins

9.0

*New players only

Play Now Read Review

5

Bonus up to:
$3000
100 Free Spins
No deposit required to claim the 100 free spins

9.0

*New players only

Play Now Read Review

6

Welcome Offer:
$8000
Bonus for New Players
Min dep: $10 Neosurf, $20 BTC, $20 LTC, $20 ETH, $20 BNB, $20 XRP, $20 DOGE, $20 Flexepin, $30 Credit Card, $40 USDT.

8.5

*New players only

Play Now Read Review

7

Wellcome Offer:
$7500
Bonus for New Players
Deposit $10 or more to claim and use bonus code WELCOME1.

9.0

*New players only

Play Now Read Review

8

Get Up to:
$5500 Bonus
Wlecome Package
Deposit $10 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

9

Get Up to:
$7777
300 Free Spins
Deposit $20 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

10

Bonus up to:
$10,000
$20 Free Chip
Use bonus code ORV20 to claim the free chip.

9.5

*New players only

Play Now Read Review

11

Get up to:
$1000
Welcome Package
Deposit $20 or more to claim the bonus.

9.5

*New players only

Play Now Read Review

12

Bonus up to:
$6000
Welcome Package
Deposit $20 or more to claim the bonus.

9.0

*New players only

Play Now Read Review

13

Get up to:
$6000
Welcome Package
Deposit $25 or more to claim the bonus.

9.3

*New players only

Play Now Read Review

14

Wellcome Offer:
555%
Bonus for New Players
Deposit $25 or more to claim the bonus.

9.0

*New players only

Play Now Read Review

15

Get Up to:
$3000
Welcome Package
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

16

Get up to:
$11,000
100 Free Spins
No deposit required to claim the 100 free spins.

8.8

*New players only

Play Now Read Review

17

Welcome Offer:
300%
Bonus for New Players
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

18

Get Up to:
$3250
Bonus for New Players
Deposit $10 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

19

Get Up to:
$7500
Welcome Package
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

20

Get Up to:
$12,000
$75 Free Chip
Deposit with bitcoin to claim the $75 free chip.

8.5

*New players only

Play Now Read Review

21

Get Up to:
$5500
Welcome Package
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

22

Get Up to:
$2000
Welcome Package
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

23

Get Up to:
$3500
30 Free Spins
Deposit $35 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

24

Get Up to:
$2500
150 Free Spins
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

25

Get Up to:
$2500
Welcome Package
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

26

Get Up to:
$1000
75 Free Spins
Deposit with crypto to claim the $75 free chip.

8.5

*New players only

Play Now Read Review

27

Welcome Offer:
400%
Bonus for New Players
Deposit $35 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

28

Get Up to:
$2550
100 Free Spins
Deposit $30 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

29

Get Up to:
$20,000
Welcome Package
Deposit $10 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

30

Get Up to:
$7500
50 Free Spins
Claim 40 free spins on 7 Chakras slot.

8.5

*New players only

Play Now Read Review

31

Get Up to:
$2000
20 Free Spins
Deposit $35 to get 200 free spins on Diamond Fiesta.

8.5

*New players only

Play Now Read Review

32

Get Up to:
$5000
150 Free Spins
Deposit $30 or more and use bonus code WILD250.

8.5

*New players only

Play Now Read Review

33

Get Up to:
$4500
$75 Free Chip
Deposit with crypto to claim the $75 free chip.

8.5

*New players only

Play Now Read Review

34

Welcome Offer:
$4500
Bonus for New Players
Deposit $20 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

35

Welcome Offer:
$777
Bonus for New Players
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

36

Welcome Offer:
$1000
Bonus for New Players
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

37

Get Up to:
$4000
20 Free Spins
Deposit $30 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

38

Get Up to:
$6000
60 Free Spins
Deposit $25 and use coupon code RICH300.

8.5

*New players only

Play Now Read Review

39

Get Up to:
$1000
60 Free Spins
Deposit $25 and use coupon code VIP300.

8.5

*New players only

Play Now Read Review

40

Get Up to:
$1000
110 Free Spins
Deposit $25 and use bonus code JUICYV200.

8.5

*New players only

Play Now Read Review

41

Get Up to:
$6000
200 Free Spins
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

42

Welcome Offer:
350%
Bonus for New Players
Deposit $30 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

43

Get Up to:
$2200
55 Free Spins
Deposit $10 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

44

Get Up to:
$1200
Welcome Bonus Package
Deposit $20 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

45

Get Up to:
$1000
Welcome Bonus Package
Deposit $20 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

46

Get Up to:
$1077
Welcome Bonus Package
Deposit $20 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

47

Get Up to:
$1000
Welcome Bonus Package
Deposit $20 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

48

Get Up to:
$800
Welcome Bonus Package
Deposit $20 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

49

Get Up to:
$1500
$50 Slots Chip
Use bonus code PRIMA50 with no deposit required.

8.5

*New players only

Play Now Read Review

50

Get Up to:
$2000
$10 Casino Chip
Deposit $50 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

51

Get Up to:
$6000
Welcome Package
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

52

Get Up to:
$1000
20 Free Spins
Deposit $20 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

53

Get Up to:
$1000
55 Free Spins
Claim 105 free spins with no deposit required.

8.5

*New players only

Play Now Read Review

54

Get Up to:
$1000
5Welcome Package
Deposit $100 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

55

Get Up to:
$14,000
Welcome Package
Deposit $10 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

56

Get Up to:
$1500
Welcome Package
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

57

Get Up to:
$1500
$25 No Deposit Bonus
Claim a $25 bonus with no deposit required.

8.5

*New players only

Play Now Read Review

58

Get Up to:
$3000
Welcome Package
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

59

Get Up to:
$2750
50 Free Spins
Deposit $30 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

60

Welcome Offer:
350%
300 Free Spins
Deposit with code THEBIG450, then claim 60 daily free spins for 5 days using the code FREE60.

8.5

*New players only

Play Now Read Review

61

Get Up to:
$2000
25 Free Spins
Claim 25 free spins bonus on Secret Symbol slot using bonus SECRET25.

8.5

*New players only

Play Now Read Review

62

Get Up to:
$3000
Welcome Package
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

63

Get Up to:
$3000
100 Free Spins
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

64

Get Up to:
$3000
Welcome Package
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

65

Welcome Offer:
400%
Bonus for New Players
Deposit $35 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

66

Welcome Offer:
250%
25 Free Spins
Claim 25 free spins using bonus code TREASURE25.

8.5

*New players only

Play Now Read Review

67

Welcome Offer:
300%
25 Free Spins
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

68

Welcome Offer:
275%
30 Free Spins
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

69

Get Up to:
$1000
35 Free Spins
Deposit $30 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

70

Get Up to:
$5000
Welcome Package
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

71

Get Up to:
$2000
Welcome Package
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

72

Get Up to:
$2500
35 Free Spins
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

73

Get Up to:
$3000
35 Free Spins
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

74

Get Up to:
$5000
$36 Free
Use bonus code FREE36USA to claim the free chips.

8.5

*New players only

Play Now Read Review

75

Get Up to:
$10,000
25 Free Spins
Use bonus code SPARKY200 to claim the bonus.

8.5

*New players only

Play Now Read Review

76

Welcome Offer:
300%
50 Free Spins
*75% Extra on Crypto Deposits or 45% Extra on MasterCard Deposits.

8.5

*New players only

Play Now Read Review

77

Get Up to:
$3000
Welcome Package
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

78

Get Up to:
$1000
100 Free Spins
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

79

Get Up to:
$5000
Welcome Offer
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

80

Get Up to:
$1110
Welcome Offer
Use bonus code WELCOME1 to claim the bonus.

8.5

*New players only

Play Now Read Review

81

Get Up to:
$2250
Welcome Offer
Deposit $30 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

82

Get Up to:
$3000
50 Free Spins
Claim 50 free spins for the Fantasy Fortune slot.

8.5

*New players only

Play Now Read Review

83

Get Up to:
$1000
Welcome Package
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

84

Welcome Offer:
250%
Bonus for New Players
Deposit $20 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

85

Welcome Offer:
450%
Bonus for New Players
Deposit $50 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

86

Welcome Offer:
200%
Bonus for New Players
Deposit $30 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

87

Welcome Offer:
$50
Bonus for New Players
Join Various Tournaments.

8.5

*New players only

Play Now Read Review

88

Get Up to:
$5000
$75 Free Chip
Deposit with crypto to claim the $75 free chip.

8.5

*New players only

Play Now Read Review

89

Get Up to:
$2500
50 Free Spins
Claim 50 free spins for the Mighty Drums slot.

8.5

*New players only

Play Now Read Review

90

Welcome Offer:
300%
Bonus for New Players
Deposit $30 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

91

Get Up to:
$11,000
25 Free Spins
Claim 25 free spins with no deposit required.

8.5

*New players only

Play Now Read Review

92

Get Up to:
$9000
Welcome Package
Deposit $35 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

93

Get Up to:
$800
Welcome Package
Deposit $25 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

94

Get Up to:
$4000
$75 Free Chip
Deposit with crypto to claim the $75 free chip.

8.5

*New players only

Play Now Read Review

95

Get Up to:
$2000
$75 Free Chip
Deposit with crypto to claim the $75 free chip.

8.5

*New players only

Play Now Read Review

96

Get Up to:
$3000
$10 Casino Chip
Deposit $45 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

97

Get Up to:
$2000
$30 Free Chip
Deposit $10 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

98

Get Up to:
$3000
Welcome Package
Deposit $20 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

99

Get Up to:
$5000
Welcome Package
Deposit $20 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

100

Get Up to:
$3000
Welcome Package
Deposit $20 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

101

Get Up to:
$1000
Welcome Package
Deposit $20 or more to claim the bonus.

8.5

*New players only

Play Now Read Review

Roulette Table Probabilities

The probabilities in an American roulette game are as follows:

• There are 38 pockets. The probability of the ball landing in either is 1/38.
• There are 18 red pockets. The probability of the ball landing in either is 18/38.
• There are 18 black pockets. The probability of the ball landing in either is 18/38.
• There are 19 pockets that are either black or green. The probability of red not occurring is 19/38.
• There are 19 pockets that are either red or green. The probability of red not occurring is 19/38.

The same kind of logic applies when calculating the probabilities found in European roulette. Instead of having 38 pockets, this variation only has 37 pockets, bringing the probability of the ball landing in either to 1/37.

How to Calculate Expected Value

In mathematics, the expected value represents the mean value of the outcomes. In this instance, it represents the mean value of the outcome of a bet in roulette. Below is a practical example of how you can calculate the expected value of any given game using American roulette probability values.

Expected Value Formula = ∑ [ x * P(x)]

Example: In roulette, a player can place a $5 bet on the number 17 and have a 1/38 probability of winning. If the ball lands on 17, the player wins $175, otherwise the casino takes the players $5. What is the expected value of the game to the player?

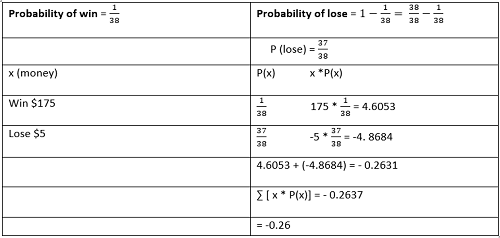
Therefore, a player who bets $5 in a single American roulette spin, can expect to lose 0.26 cents in that round. The same formula and logic can be used for calculating the expected value of any given game using European roulette probability values.

Other Roulette Guides

• Roulette Odds
• European Roulette
• French Roulette
• American Roulette
• Roulette Bets
• Mini Roulette
• Royale Roulette
• Riveboat Roulette
• Roulette Computer
• Roulette Cheats
• Casino Roulette
• Roulette Systems
• Roulette Lessons
• Zoom Roulette
• Roulette Tips
• Martingale Systems
• Fibonacci System
• James Bond Strategy
• Oscar Grind’s Strategy
• d’Alembert System
• Paroli System
• Parlay Roulette System
• Roulette Strategies
• Roulette Bets
• How to Win Roulette
• Roulette Bonses
• Multiplayer Roulette